Обложка / Оглавление

– Причем здесь роза? Это какая-то ошибка.
– А с чем еще я могу сравнить математику? |
Математика и естествознание
Тем, кому интересно, как
создается новая книга по математике, можем порекомендовать последить за
развитием проекта В. Меркатора  .
Книги пока еще не существует. Более того, нет полного понимания, как сделать
хорошую книгу в электронном формате. Трудно обещать при подобных
обстоятельствах, что проект окажется интересным, и что он непременно
закончится удачно. Тем не менее мы ничего не потеряем, если проявим к этому
проекту интерес. К тому же сама теория тензоров – одна из интереснейших
математических теорий. .
Книги пока еще не существует. Более того, нет полного понимания, как сделать
хорошую книгу в электронном формате. Трудно обещать при подобных
обстоятельствах, что проект окажется интересным, и что он непременно
закончится удачно. Тем не менее мы ничего не потеряем, если проявим к этому
проекту интерес. К тому же сама теория тензоров – одна из интереснейших
математических теорий.
Что такое математика?
|
Математика и естествознание
Существуют вопросы, на которые на сегодняшний день нет
возможности дать однозначный ответ. Скажем, у нас нет достаточных оснований
предполагать, что мы во Вселенной не одиноки. В то же время мы не можем доказать
и обратное. В таких случаях мы можем говорить только о тех или иных
существующих точках зрения по поводу спорного вопроса. Каждая из точек зрения
непременно каким-либо образом обосновывается, иначе она не может приниматься в
расчет. В то же время это обоснование не может быть стопроцентным, так как
иначе осталась бы только одна точка зрения, и вопрос перешел бы из разряда
спорных в разряд вопросов, имеющих точное строго доказанное решение.
На математику существуют две основные точки зрения, суть
которых отражена в следующей таблице.
Математика не относится к
естественным наукам.
| Математика – наука о наиболее
общих законах природы.
|
"Математику нельзя причислить
к естествознанию или общественным наукам: естествознание непосредственно
изучает природу, а математика изучает не сами объекты действительности, но
математические объекты, которые могут иметь прообразы в
действительности" [41, Бондарев, с. 48].
Т.е. объекты, которые изучает
математика, могут иметь отношение к действительности, а могут и не иметь, но
зачем же тогда мы их изучаем?
| "Чистая математика имеет
своим объектом пространственные формы и количественные отношения
действительного мира, стало быть – весьма реальный материал. Тот факт, что
этот материал принимает чрезвычайно абстрактную форму, может лишь слабо
затушевать его происхождение из внешнего мира" [Антидьюринг, с. 33].
|
"Математика (в пер. с греч.
означает знание) – наука о математических структурах (множествах, между
элементами которых определены некоторые отношения)" [40, Философский словарь
(краткий), с. 266].
| "Дело в том, что математика
возникла именно как инструмент наиболее общего и объективного, а значит, и
наиболее абстрактного и формального описания законов природы"
[45, А. Зенкин (профессор, доктор
физико-математических наук, ведущий научный сотрудник Вычислительного центра
РАН) "НАУЧНАЯ КОНТРРЕВОЛЮЦИЯ В МАТЕМАТИКЕ"].
|
"Математика в естествознании
играет роль универсального языка, специально предназначенного для
лаконичной точной записи различных утверждений" [41, Бондарев, с. 53].
| "Все попытки избежать
вмешательства реального мира в математику – сектантство, которое
восстанавливает против себя любого разумного человека и вызывает у него
отвращение к этой науке, к умножению и к любым доказательствам. Подобное
"абстрактное" описание математики непригодно ни для обучения, ни
для каких-либо практических приложений" [43, Арнольд].
|
"Точки зрения современных
математиков на природу своей науки отражены в недавно вышедшей книге,
изданной Международным математическим союзом в 2000 году "Математика:
границы и перспективы". Один из самых знаменитых математиков объясняет
там: математика – это раздел филологии, основанный на своеобразной
грамматике (в которой, например 1+1=2, что составляет теорему 110.643 в
"Принципах математики" Рассела и Уайтхеда")" [44, Из
статьи Владимира Игоревича Арнольда – Президента Московского математического
общества, академика РАН, профессора университета Париж-Дофин, Франция,
главного научного сотрудника Математического института РАН, иностранного члена
Французской АН, Национальной АН США, Лондонского королевского общества и
Accademia dei Lincei в Риме, члена американской Академии искусств и наук,
почетного доктора многих зарубежных университетов, одного из крупнейших
математиков современности].
| Есть в математике традиционные
трудности, о которых все знают, но ничего поделать не могут. Впервые такую
проблему обнаружил Зенон Элейский почти двадцать четыре века назад. Если
строго следовать строгой математической логике рассуждений, то можно
доказать, что Ахилл никогда не догонит черепаху. Зенон даже доказал, что он
вообще не сможет сдвинуться с места. Он доказал, что движения не существует.
Рассуждения Зенона абсолютно
строги и непротиворечивы. Во всяком случае так можно было считать на
протяжении 23 столетий из 24, на протяжении которых эти апории известны
математикам. Если бы математика была бы абсолютно независима от
естествознания, то эти апории логично было бы рассматривать как строго
доказанные теоремы и включить во все учебники математики. Однако таких попыток
никто никогда не предпринимал, на протяжении 23 столетий. Почему? Потому, что
вывод этих "теорем" находится в вопиющем противоречии со всеми теми
знаниями о природе, которые мы имеем.
Возможно это самый яркий пример
зависимости математического знания от опыта.
|
"Математика дает самый
блестящий пример чистого разума, удачно расширяющегося самопроизвольно, без
помощи опыта".
(Из реферата аспирантки Мехмата
МГУ).
Эта цитата чрезвычайно
показательна: с одной стороны, это мнение аспирантки Мехмата МГУ – учебного
заведения, где по определению дают самое лучшее математическое образование в
мире; с другой стороны, это мнение аспирантки, у которой пока еще нет
собственного опыта, и, поэтому, можно считать, что оно отражает некое
усредненное мнение, бытующее в студенческо-преподавательской среде и это
мнение естественно возникло не на пустом месте.
"Математика есть создание
чистого разума и поэтому не нуждается в связях с другими сферами деятельности
человека" [Л. Морделл, 5, с. 31]
| "Глубокое изучение природы –
вот самый обильный источник математических открытий".
Фурье [5, с 31].
|
"Математик изучает понятия,
которые сам же и создает" [29, Альфред Реньи, венгерский математик с.
33].
"Математика, занимающаяся
изучением воображаемых, не существующих в природе объектов, именно поэтому и
может устанавливать о них истину, что эти объекты такие, какими мы их
создаем" [29, Альфред Реньи, с. 32].
|
|
"Математика с нашей точки
зрения, не наука – в том смысле, что она не относится к естественным наукам.
Ведь мерило ее справедливости отнюдь не опыт".
Фейнман.
[26, с. 56].
|
|
"Для математической мысли
характерно, что она не выражает истину о внешнем мире, а связана
исключительно с умственными построениями".
Гейтинг А. Интуиционизм.
[48, с. 17].
|
|
"... в принципе современная
математика в основе своей не имеет какой-либо утилитарной цели, а
представляет собой интеллектуальную дисциплину, практическая польза которой
сводится к нулю... математик в своих исследованиях никогда не руководствуется
мыслью о степени полезности полученных результатов в будущем (что, впрочем, и
невозможно предсказать), скорее он руководствуется желанием проникнуть в
понимание математического явления, как явления, заканчивающегося на себе
самом ... математика – не более чем "роскошь", которую может позволить
себе цивилизация"
Ж. Дьедоне [5, с. 31].
Блехман И.И., Мышкис А.Д., Пановко
Я.Г. Механика и прикладная математика: Логика и особенности приложений
математики. [5]
|
|
Несложно заметить, что высказываний в пользу особого
положения математики в системе наук найти гораздо легче. Это не удивляет, ведь
особенность математики как научной дисциплины выглядит достаточно очевидной.
Удивляет другое, почему при явной очевидности данного факта, существует тем не
менее иное мнение, которого придерживаются в том числе и некоторые видные
математики.
Аргументация тех, кто считает "математику самым
блестящим примером чистого разума, удачно расширяющегося самопроизвольно, без
помощи опыта", вполне понятна. Но что мы можем сказать в защиту
противоположной точки зрения? Мы помним, что строгого решения этой проблемы не
существует. В то же время дать несколько ярких примеров в пользу математики,
как одной из наук о природе, мы можем.
Начнем с математических парадоксов, которые бывают двух
типов: софизмы и настоящие парадоксы – апории. Софизмы не являются настоящими
парадоксами – это математические фокусы.
Точное определение софизма из словаря.
Софизм – правильное по форме, но приводящее к
неверному по существу результату рассуждение.
Феликс Клейн приводит софизм, в котором при помощи
специальным образом построенного чертежа доказывается, что все треугольники
равнобедренные.
Вот
этот чертеж
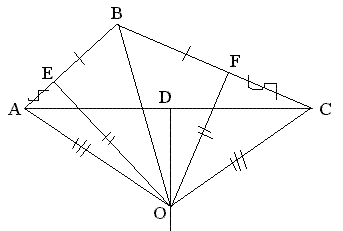
ABC – произвольный треугольник;
BC – биссектриса;
DO – высота, восстановленная из середины стороны AC.
Чтобы опровергнуть этот софизм, необходимо очень аккуратно
выполнить чертеж. Но как утверждает Феликс Клейн, если мы хотим построить
геометрию, как логическую науку, она не должна нуждаться "неизбежным
образом для установления своих выводов в апеллировании к интуиции и чертежам
после введения аксиом" [Феликс Клейн, с. 310]. Почему? Да потому, что в
этом случае справедливость, доказанных в математике теорем, очевидным образом
зависит от объективной действительности в форме грубого чертежа.
Инженеры и физики не склонны видеть в этом недостаток, так
как именно для изучения грубой действительности они обычно и используют
математику. Они до сих пор пользуются геометрией Евклида, хотя недовольный этой
геометрией Давид Гильберт уже давно изобрел ее усовершенствованный вариант.
Второй пример, который может быть является наиболее сильным
аргументом в пользу того, что математики это наука о природе, мы уже отметили в
нашей таблице. Речь идет об апориях Зенона.
Зенону почти двадцать четыре века назад удалось совершенно
строго доказать, что Ахилл никогда не догонит черепаху. Зенон даже доказал, что
Ахилл вообще не сможет сдвинуться с места и что движения не существует.
Рассуждения Зенона абсолютно строги
и непротиворечивы. Во всяком случае так можно было считать на протяжении 23
столетий из 24, на протяжении которых эти апории известны математикам. Если бы
математика была бы абсолютно независима от естествознания, то эти апории
логично было бы рассматривать как строго доказанные теоремы и включить во все
учебники математики. Однако таких попыток никто никогда не предпринимал, на
протяжении 24 столетий. Почему? Потому, что вывод этих "теорем"
находится в вопиющем противоречии со всеми теми знаниями о природе, которые мы
имеем. Следовательно, апории Зенона не были признаны правильными теоремами только
в силу того, что они не удовлетворяли экспериментальной проверке.
Возможно это самый яркий пример зависимости математического
знания от опыта.
Следующие примеры связаны с понятием бесконечности в
математике.
Определение. Философский словарь.
Бесконечность – философская
категория, характеризующая неисчерпаемость материи и движения, многообразие
явлений и предметов материального мира, форм и тенденций его развития.
|
В математике под бесконечностью понимают то, что Гегель
называл скучной бесконечностью. Когда математики говорят о бесконечном, то
обычно подразумевается нескончаемый ряд однородных или одинаковых элементов.
Понятие бесконечности вошло в науку и, прежде всего, в
математику давно. Особое значение это понятие приобрело с изобретением
математического анализа Ньютоном и Лейбницем. Дело в том, что в математическом
анализе понятия бесконечно большого и бесконечно малого становятся основными.
Математики даже начали говорить, что математика – это наука о бесконечном.
Но бесконечного не бывает в природе и не встречается в
человеческой практике. Бесконечное является обязательным атрибутом чего-то
сверхъестественного, загадочного, божественного. Все это в очередной раз
наталкивает на мысль об исключительном положении математики. Но прежде чем
делать какие-либо выводы, присмотримся к этому понятию поближе.
Конечно, бесконечного в природе мы не встречали, но также
несомненно, что наше понятие о бесконечном происходит от представления о чем-то
очень большом или о чем-то очень продолжительном. Пусть у нас имеется очень большое
количество чего-либо. Какое самое главное свойство такого очень большого
количества мы можем отметить? Допустим, что мы говорим о количестве капель в
море. Мы понимаем, что строго говоря если мы отнимем у моря или добавим в него
несколько капель, то его уровень должен измениться очень, очень незначительно.
Очевидно, однако, что для всех имеющих практическое значение задач мы можем
считать, что уровень моря остается постоянным при добавлении в него конечного и
иногда даже очень большого количества капель.
Когда мы имеем дело с чем-то очень большим, то мы можем не
считаться с небольшими колебаниями его количества. От большого не убудет если
мы слегка от него отнимем. Конечно это не совсем так, но во многих случаях
такое упрощение оправдано. Абсолютизируя это свойство, мы приходим к понятию
бесконечного.
Несколько примеров, демонстрирующих как понятие о
неисчерпаемости бесконечного упрощает в некоторых случаях решение конкретных
задач.
Задача первая. Сумма геометрической прогрессии.
Сумма членов геометрической прогрессии.
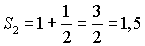 ;
;
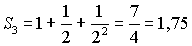 ;
;
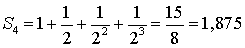 ;
;
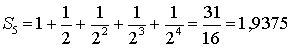 .
.
Чем больше членов прогрессии требуется сложить, тем труднее
вычислить сумму. А если требуется вычислить сумму сотни или тысячи членов
прогрессии? Но из полученных выражений уже видно, что чем больше членов мы
учитываем, тем менее различаются результаты. Видимо, если нам не нужна особая
точность, для большого количества членов прогрессии можно воспользоваться более
простой формулой, которую мы можем получить предположив, что членов бесконечно
много.
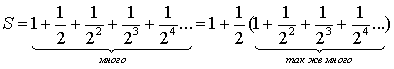 .
.
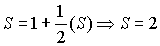 .
.
То есть при большом или бесконечном количестве членов
прогрессии можно считать, что сумма точно равна двум. Получается, что бесконечное
количество членов прогрессии сложить гораздо проще, чем конечное.
Еще один пример из математики. При вычислении площади
правильных многоугольников с очень большим числом сторон встречаются выражения
вида:
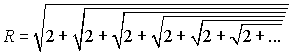 .
.
Воспользуемся тем же приемом: будем считать, что эта
последовательность радикалов бесконечна. Тогда:
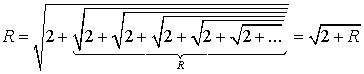 .
.
Решая это уравнение, получим:
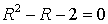 ,
,
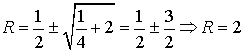 .
.
Снова для бесконечной последовательности результат получается
более простым.
Пример из физики.
Вычислить сопротивление электрической цепи с большим
количеством звеньев. Такие задачи встречаются в теории линий электропередачи и
линий связи.
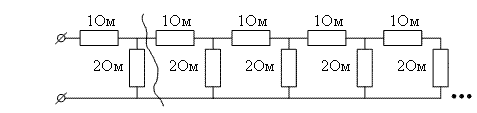
Упростим задачу. Будем считать, что схема бесконечно
длинная, тогда, если мы отнимем от нее два первых сопротивления, то ее
сопротивление не изменится, так как оставшаяся схема точно такая же, как и
начальная. Следовательно, мы можем всю схему заменить эквивалентной.
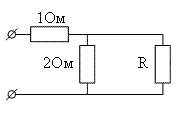
Эту схему уже гораздо легче рассчитать. Помня, что полное
сопротивление всей схемы равно сопротивлению отброшенной и замененной на
эквивалентное сопротивление R части, получим:
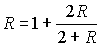 ,
,
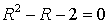 ,
,
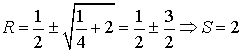 .
.
Подобных примеров в науке, когда понятие бесконечности
оказывается полезным и в конечном итоге упрощает расчеты, множество.
Свойство неисчерпаемости "скучной" бесконечности
настолько характерно, что в современной математике взято за ее определение.
Математики говорят, что бесконечное не изменится если мы отнимем от него какое
угодно конечное количество его элементов. Оставшееся при этом множество в
количественном отношении будет тождественно первоначальному. В то же время,
поскольку оно тождественно некоторой части первоначального множества, говорят,
что бесконечное подмножество эквивалентно некоторому своему подмножеству.
Другими словами бесконечное в количественном отношении
эквивалентно некоторой своей части. В природе такое в самом деле не
встречается. Настоящее никогда не заканчивающееся бесконечное встречается
только в математике. И тем не менее это не повод для того, чтобы отнести
математику к особенным наукам. Аналогичное положение вещей характерно для любой
науки вообще. Любая теоретическая наука оперирует понятиями, не имеющими
непосредственных аналогов в природе. Теоретические понятия всегда
идеализированы и упрощены. Например, в теоретической механике мы изучаем законы
движения абсолютно твердых тел. Таких не существует в природе. Более того, иногда
это понятие может приводить к противоречиям и парадоксам. Тем не менее это
никого не пугает, просто все знают, что каждое теоретическое понятие имеет свою
область применения. Если нам необходимо учесть деформации тел, то следует
обратиться к другим теориям, в частности к теории упругости. Теория упругости
оперирует абсолютно упругими телами, которых, кстати, тоже нет в природе. Тем
не менее, с определенным классом задач эта теория справляется.
К противоречиям может привести и неосторожное обращение с математическими
бесконечностями. В частности задача на вычисление энергии иона в
кристаллической решетке может привести к проблеме суммирования условно
сходящегося знакопеременного ряда. Сумма такого ряда может быть любой, в
зависимости от порядка в котором складываются члены ряда. В то же время с
физической точки зрения энергия иона должна иметь единственное значение.
Приведенные примеры показывают, что для математики
характерны те же самые проблемы, что и для других естественных наук, а ее
понятия, даже такие экзотические, как бесконечность, имеют природное
происхождение.
Как же тогда могло сложиться представление об особенном
характере математического знания? Попытаемся подойти к этой проблеме
исторически.
Известно, что древние греки, с которых начинается
современная математика, были рабовладельцами. Они презирали физический труд и
всякого рода экспериментирование. Использование математики для решения
каких-либо практических задач считалось делом недостойным свободного человека.
Архимед, один из древнегреческих ученых, который использовал свои знания для
создания механических устройств, в частности он сделал расчет баллист
использовавшихся при обороне его родного города Сиракузы. По преданию, он
просил солдат, которые, в конце концов, захватили город и пришли его убить, не
трогать его ученые записи. Опять же по преданию известно, что в этих записях,
которыми он так дорожил, он не нашел нужным описать ни одного из
сконструированных им устройств, считая это презренным делом. Плутарх об этом
пишет так:
"Хотя эти изобретения заслужили ему репутацию
сверхчеловеческой проницательности, он не снизошел до того, чтобы оставить
какое-либо писанное сочинение по таким вопросам, а, считая низким и недостойным
делом механику и искусство любого рода, если оно имеет целью пользу и выгоду,
все свои честолюбивые притязания он основывал на тех умозрениях, красота и
тонкость которых не запятнаны какой-либо примесью обычных житейских нужд"
[Стройк, с. 69].
Древнегреческая наука признавала только один способ
доказательств – теоретический. Эксперимент же считался делом рабов
[Космодемьянский, с. 57].
Одним из шедевров древнегреческой науки считается геометрия
Евклида, в которой, отталкиваясь от нескольких очевидных истин, строго
доказательно строится вся система теорем, составляющая основное содержание
теории. По существу, эту геометрию мы до сих пор изучаем в школе. На протяжении
многих веков геометрия Евклида считалась образцом точной и строгой
математической теории. Эта теория не нуждалась в экспериментировании для своего
обоснования. Истины, на которых она строилась, были настолько очевидны, что
воспринимались как известные всем от рождения. Религиозный человек
средневековья воспринимал аксиомы, как непосредственное знание, данное нам от
Бога. Представление об априорном независимом от опыта знании было развито и
закреплено религиозной философией и освящено авторитетом Церкви.
Очевидность аксиом геометрии не вызывает сомнения даже у
современного человека. Аксиомы действительно очевидны, и невозможно даже
представить, что может быть как-то иначе.
Первыми математиками,
которые усомнились в очевидности аксиом Евклида (аксиомы о параллельных) были
русский Николай Иванович Лобачевский (1830 г.), ректор Казанского университета,
и венгр, Янош Бояи (1832 г.). Карл Фридрих Гаусс (1777–1855), который,
видимо, раньше других пришел к аналогичным выводам, никогда не публиковал работ
на эту тему, считая, что современники все равно его не поймут. Он оказался
прав: ни на работу Лобачевского, ни на работу Бояи современники внимания не
обратили и не поняли. Из этих троих математиков двое, Лобачевский и Гаусс,
предприняли попытки экспериментальной проверки аксиомы о параллельных. Я не
знаю других примеров из истории, когда математики пытались обратиться к
эксперименту для установления математической истины.
Неевклидовы геометрии
получили признание только после работ Георга Фридерика Бернгарда Римана (1854
г.). По Риману неевклидова геометрия является внутренней геометрией
криволинейных поверхностей. Работа Римана открыла математикам множество
геометрий, но оставила в стороне вопрос о том, какая из них может считаться
геометрией нашего мира.
Открытие неевклидовых
геометрий подорвало репутацию аксиом как очевидных истин. Казалось бы, что
следующий шаг, который должен быть сделан – это отказ от идеи априорного знания
и признание опытного происхождения истин, которые совсем недавно считались
очевидными.
В самом деле. Откуда берутся очевидные истины? Как могла
появиться идея врожденного знания, которая оказалась столь живучей, что даже
сегодня многие в нее верят? Человек, родившись, еще не умеет думать и не умеет
говорить и у него еще пока нет сознания. Если в этот момент его лишить
человеческого общения (такие примеры в истории встречались), то сознание так и
не возникнет. Это говорит о том, что никаких врожденных идей у него нет. Первые
несколько лет он изучает язык и одновременно учится думать. Вместе с языком он
впитывает первые представления о мире. Эти знания добыты многотысячелетней
практикой и закрепились в языке и в человеческой культуре. В результате этого
обучения возникает мышление. Когда мышление рождается, человек уже многое знает
о мире. Очевидные истины действительно являются врожденными, но только
рождаются они вместе с рождением мышления.
Очевидные истины – это фундаментальные знания
самого общего характера о мире, которые добыты общечеловеческой практикой на
протяжении тысячелетий и закреплены в языке.
|
Именно поэтому эти истины каждым из нас воспринимаются как
врожденные и именно поэтому они не являются на сто процентов надежными.
Следовательно, математику можно определить как науку,
которая изучает наиболее общие свойства нашего мира исключительно
теоретическими методами, опираясь на эмпирические знания, зафиксированные в
языке, добытые тысячелетней практикой всего человечества и на опыт других
естественных наук.
|
Математикам не нужно ставить своих экспериментов только
потому, что за них это давно сделали другие. Основная задача математиков
сделать из этих экспериментов правильные выводы.
Это объясняет "непостижимую" эффективность. Это
объясняет также широкое использование математики и ее специфического языка в
других естественных науках.
Древние греки, которые изобрели теоретическую науку, сняли
пенки с многовекового эмпирического познания человечества. Древнегреческая
механика также как и математика была умозрительной наукой. Архимед строит
теорию рычага, основываясь на четырех допущениях, которые считает очевидными:
1. Равные грузы, приложенные к равным плечам рычага,
уравновешиваются.
2. Равные грузы, приложенные к неравным плечам рычага, на
находятся в равновесии. Груз, приложенный к более длинному плечу, падает вниз.
3. Если грузы, подвешенные на каких-нибудь плечах рычага,
находятся в равновесии, то, если к одному из грузов что-либо добавить,
равновесие нарушится и груз, к которому прибавлено, будет падать вниз.
4. Точно так же, если от одного груза отнять что-либо, то
равновесие нарушится и груз, от которого не было отнято, падает вниз.
Отталкиваясь от этих аксиом, Архимед получил условие
равновесия рычага:
"Любые грузы находятся в равновесии, когда плечи рычага
обратно пропорциональны грузам"
Аксиомы механики носят ярко выраженный экспериментальный
характер. Вместе с тем Архимед использует общий для всей древнегреческой науки
метод сведения доказательства к нескольким очевидным истинам.
Древние греки вышли в некоторых случаях на рубежи, на
которых дальнейшее познание невозможно было без экспериментальных исследований:
механика, гидростатика, астрономия, представления о непрерывном движении и
бесконечно делимом пространстве. Но решительного поворота к экспериментальному
познанию они не сделали.
Однако уже Галилей (1564–1642) сделал механику
экспериментальной наукой. Крылатая фраза, что "наука начинается с
измерения" принадлежит Д.И. Менделееву, но уже Галилей говорил почти
то же самое, но другими словами. С этого момента естественные науки начинают
все более стремительно размежевываться с математикой и философией по методам
исследования.
Таким образом, и математика и физика столкнулась с
одинаковыми проблемами ненадежности очевидных истин. Физика при этом стала
наукой экспериментальной, а математика предпочла другой путь развития.
Слишком привычными и
привлекательными были освещенные веками идеи существования априорного знания,
абсолютной точности и непогрешимости математики. Все эти идеи никак не
вяжутся с грубым и неточным экспериментом. Согласиться на то, что в основании
математики лежат грубые экспериментальные истины, математики не могли. Гораздо
более привлекательным казался путь, при котором аксиомы рассматривались как
произвольные формальные утверждения. Математики сняли с себя ответственность за
содержательную истинность аксиом. Аксиомы не понимаются более как очевидные
истины, и в то же время они по-прежнему не нуждаются в доказательствах. Это
просто некоторые утверждения ни о чем. Природа изучаемых объектов в строгой
аксиоматической теории не имеет значения – аксиомы определяют отношения между
объектами, чья природа, как и названия безразличны. В беседах Гильберт не
раз шутя говорил, что в геометрии вместо точек, прямых, плоскостей можно было
бы говорить о столах, стульях и кружках пива.
Содержание аксиом к математике не относится. Математикой
теперь считается только умение формально правильно получать формальные
следствия из формальных аксиом. Конечно, при таком подходе математика не
является естественной наукой. Такой подход достаточно долго превалировал в
математике, чем и можно объяснить сложившееся о ней мнение.
К счастью, всегда существовали специалисты, которые таких
взглядов на математику не разделяли.
Нельзя считать, что формальный подход к математике
совершенно не оправдан. Следует признать, что он оказался полезен во многих
отношениях, в частности повысилось представление об уровне строгости
математических доказательств, математические теории стали более универсальны...
В то же время многие отмечают и негативные стороны длительно
развития математики как формальной науки.
Приведем примеры таких мнений.
"Лет тридцать тому назад ради спортивного интереса я
начал коллекционировать различные "логики", используемые в
современных логико-математических трактатах. Когда их количество перешагнуло
вторую сотню, стало ясно: если логику можно выбирать "по вкусу" (или
даже конструировать "по потребности"), то такое понятие, как
"наука", становится здесь просто неуместным" [45, Александр Александрович
Зенкин, профессор, доктор физико-математических наук, ведущий научный сотрудник
Вычислительного центра РАН].
"Обучение математике, как своеобразной юридической
казуистике, основанной на произвольно выбранных законах, начинается с самого
раннего возраста" [44, Арнольд].
"Теория множеств открыла путь к изучению необъятного
количества различных структур и к беспрецедентному росту знаний относительно
них. Это привело к распылению математики. ... Математика, основанная на
канторовской теории множеств, превратилась в математику канторовской теории
множеств. Канторовская теория ответственна за это ущербное развитие математики;
...Все структуры, изучаемые в современной математике, априорно жестко заданы, и
роль математика есть просто роль наблюдателя, их описывающего. Именно поэтому
математики столь беспомощны в постижении таких неточных по самой своей природе
понятий, как реализуемость, взаимоотношение непрерывного и дискретного и т. д.
Современная математика
изучает, таким образом, конструкцию, отношение которой к реальному миру по
меньшей мере проблематично. Более того, эта конструкция не единственно
возможная, да и на самом деле не самая подходящая с точки зрения самой
математики. Это ставит под вопрос роль
математики как научного и полезного метода. Математика может быть
низведена к простой игре, происходящей в некотором специфическом искусственном
мире. Это не опасность для математики в будущем, а непосредственный кризис
современной математики. Он проявляется и в том, что часто глубокие и остроумные
математические результаты не вызывают никакого интереса не только у людей,
которые не являются математиками-профессионалами, но даже у математиков, в
настоящее время работающих над проблемами с другим расположением фигур на
шахматной доске"
[46, Вопенка П. Математика в альтернативной теории множеств]
Что можно сказать о взгляде на математику как на особый
язык?
Что касается о взгляде на математику как на особый язык,
специально предназначенный для точного описания природы, то вряд ли с этим
можно согласиться, поскольку нельзя изобрести весь язык целиком. Язык возникает
только при необходимости отобразить в его знаках некоторое знание. По мере
накопления, расширения, углубления нашего знания о природе в языке возникают
новые структуры, которые нельзя придумать изначально. Любая естественная наука
создает и развивает свой собственный язык, и математика не является в этом
исключением. Но математика вряд ли бы смогла так успешно развивать свой язык,
если бы она не добывала все время новое знание о своем предмете исследования:
ей просто незачем было бы это делать.
Вывод.
Математика принципиально не отличается от других
естественных наук, поэтому нет никакого смысла в ее особом статусе.
Сайт управляется системой
uCoz
![]() .
Книги пока еще не существует. Более того, нет полного понимания, как сделать
хорошую книгу в электронном формате. Трудно обещать при подобных
обстоятельствах, что проект окажется интересным, и что он непременно
закончится удачно. Тем не менее мы ничего не потеряем, если проявим к этому
проекту интерес. К тому же сама теория тензоров – одна из интереснейших
математических теорий.
.
Книги пока еще не существует. Более того, нет полного понимания, как сделать
хорошую книгу в электронном формате. Трудно обещать при подобных
обстоятельствах, что проект окажется интересным, и что он непременно
закончится удачно. Тем не менее мы ничего не потеряем, если проявим к этому
проекту интерес. К тому же сама теория тензоров – одна из интереснейших
математических теорий. 
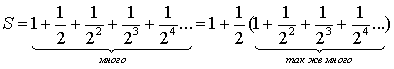 .
.
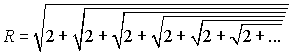 .
.
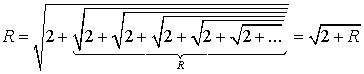 .
.
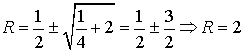 .
.


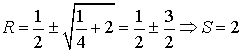 .
.