Классический радиус электрона

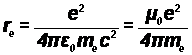 = 2.817 940 92∙10^-15 м.

 

Понятие классического радиуса электрона основано на допущении того, что энергия покоя электрона равна его электростатической энергии. Для того, чтобы собрать заряд равный заряду электрона внутри некоторой сферы, необходимо совершить работу против сил электростатического отталкивания. Найдем работу этих сил. Для этого, следуя совету Фейнмана, будем наслаивать последовательно друг на друга сферические слои бесконечно малой толщины. Каждый раз, перемещая на уже построенную сферу радиуса r, очередной тонкий слой объемом dV, мы будем помещать на нее заряд dq.

 

 

Поскольку объем оболочки равен , то , где ρ – плотность заряда внутри электрона. Здесь мы сделаем допущение, что плотность заряда внутри электрона всюду одинакова. Тогда величина заряда внутри уже собранной сферы определится как .

Мы можем найти потенциал на поверхности этой сферы

.

 

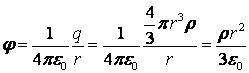Тогда работа, которую требуется совершить, а, следовательно, и энергия которую приобретает сфера, может быть найдена по формуле: . Учитывая найденные значения для φ и dq, мы получаем:

.

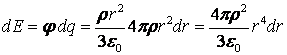Продолжаем этот процесс вплоть до неизвестного пока еще радиуса электрона .

Полную электростатическую энергию электрона мы найдем как интеграл

.

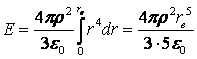Полученное выражение неудобно тем, что в него входит неизвестное значение плотности заряда ρ. Ее придется выразить через величину заряда электрона и объем.

.

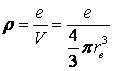Следовательно,

 

.

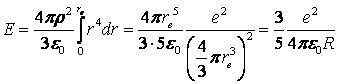Теперь приравняем полученное значение для электростатической энергии к энергии покоя электрона .

Интерес в данном случае представляет только порядок величины, поскольку наше предположение о постоянной плотности внутри электрона ни на чем не основано. Поэтому, пренебрегая коэффициентом , получаем .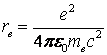

Теперь вспомнив, что 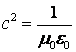, получим еще одно выражение для радиуса:

.

 

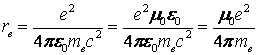И окончательно:

.

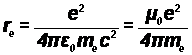Эти выражения, считаются определениями классического радиуса электрона.

 

С точки зрения современной науки понятие радиуса электрона не имеет смысла, поскольку во всех известных экспериментах электрон проявляет себя как бесструктурная точечная частица.

 

Интересно, что если использовать полученную формулу для вычисления радиуса протона, то мы получим во столько раз меньшую величину, во сколько масса протона больше массы электрона.

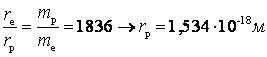
Получается, что протон в 1836 раз меньше точечного электрона и при этом он состоит из трех кварков, настолько массивных, что они не могут существовать в свободном состоянии.