Парадокс близнецов

"Парадокс часов", он же "парадокс близнецов", был сформулирован в 1912 году Полем Ланжевеном через 7 лет после создания специальной теории относительности. (Данную информацию я почерпнул у Владимира Макаровича Мясникова на его персональном сайте http://quater1.narod.ru/index.html.) Задачка оказалась трудная. Какое-то время даже считалось, что в рамках специальной теории относительности парадокс разрешить нельзя. Конечно, когда на теорию навалились математики, этот и другие парадоксы были разрешены. Но не зря Эйнштейн сам признавался, что с тех пор, как за теорию относительности принялись математики, он ее уже сам не понимает. Те объяснения парадокса, которые мне встречались, на мой взгляд, очень сложные. Далее я собираюсь изложить элементарное решение для парадокса. Мне оно кажется проще, хотя утверждать это я не берусь. Во всяком случае, раз оно мне кажется проще, возможно, покажется проще кому-то еще.

Напомню содержание парадокса.

Два близнеца живут на Земле. Один из них отправляется в дальний космический полет. Согласно специальной теории относительности в движущейся системе отсчета время идет медленнее по сравнению с неподвижной. Поэтому космонавт, вернувшийся из далекого полета, который протекал при очень большой скорости (если скорость мала, эффект будет незаметен), будет моложе своего брата, остававшегося на Земле. С другой стороны, с точки зрения космонавта, все время полета двигалась по отношению к нему Земля. Следовательно, часы должны идти медленнее у его брата, оставшегося на Земле. Выходит, что брат, который никуда не летал, и все это время оставался на Земле, должен при встрече быть моложе своего брата-космонавта. Но не могут оба брата быть одновременно один моложе другого – возникает противоречие.

Для того, чтобы рассудить братьев, придется пережить события за каждого из них. Начнем с более простого случая и проследим за процессами с Земли. Систему отсчета, связанную с Землей, будем считать условно неподвижной или просто неподвижной.

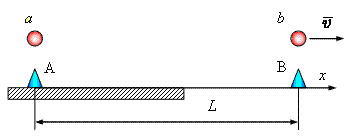
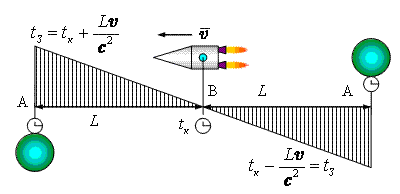
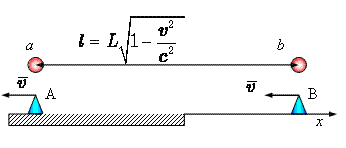
Для того, чтобы проще было рисовать брата-космонавта будем изображать шариком, а брата-наблюдателя – конусом. Пусть x – ось, связанная с неподвижной системой координат. В точках A и B неподвижной оси расположены наблюдатели. Пусть наблюдатель B расположен как раз в той точке, долетев до которой космонавт останавливается и поворачивает обратно. Будем считать, что остановка и поворот происходят мгновенно. С точки зрения земного наблюдателя все его часы синхронизированы и показывают одно и то же время. Расстояние до точки B по земным меркам равно L. Буквами a и b обозначен космонавт в начальном и в конечном пунктах своего путешествия. Когда космонавт доберется до наблюдательного пункта B, часы земного наблюдателя в его системе координат будут показывать одно и то же время .

Часы космонавта идут медленнее и, поэтому, в точке B они будут показывать меньшее время .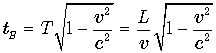

Теперь заметим, что когда космонавт пролетает непосредственно над пунктом B, наблюдатель, который находится в этом месте, может непосредственно рассмотреть часы космонавта и убедиться в том, что его часы показывают данное время. То же самое можно сказать о космонавте. Следовательно, показания часов наблюдателя и космонавта в пункте B будут иметь именно это значение из любой системы отсчета: инерциальной или нет. Пусть теперь космонавт резко остановится. На показаниях часов в точке B это никак не может отразиться, даже если они сломаются. Когда космонавт придет в себя и сможет сопоставить показания своих часов с показаниями земного наблюдателя, сразу станет ясно, что он моложе своего брата. Для большей убедительности он может повторить путешествие в обратном направлении и при этом он выиграет ровно столько же времени.

Когда космонавт вернется в пункт A, его часы будут показывать время 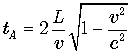. Часы земного брата покажут соответственно . Следовательно, космонавт моложе .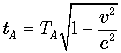

Посмотрим теперь на события глазами космонавта.

С его точки зрения неподвижные наблюдатели движутся относительно него со скоростью . Собственное расстояние между наблюдателями равно L, но космонавт видит их на расстоянии

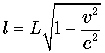. Для того, чтобы преодолеть это расстояние, наблюдателю A пришлось затратить время 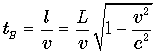. Именно это время и должны показывать часы космонавта, когда он достигнет наблюдателя B. Этот результат находится в полном соответствии с результатом каждого земного наблюдателя. Часы земного наблюдателя в точке B космонавт может наблюдать непосредственно и, поэтому, его точка зрения на то, что он видит, не должна расходиться с точкой зрения земного наблюдателя B относительно показаний своих собственных часов. Наблюдатель B знает, что когда он встретил космонавта, его часы показывали время равное , следовательно, такое же время увидит и космонавт. Показания часов космонавта и наблюдателя B известны им обоим и, если теперь космонавта мгновенно затормозить, показания часов не успеют измениться. Следовательно, космонавт, остановленный в точке B, будет моложе и с точки зрения космонавта.

Изменим теперь направление движения космонавта. С точки зрения космонавта в этом случае наблюдатель A будет приближаться к нему со скоростью . Расстояние от A до космонавта в начальный момент движения, когда космонавту придали уже скорость в обратном направлении, будет равна 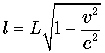. Следовательно, как и ожидалось, на обратный путь космонавт затратит время 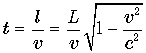. Полное время на все путешествие в прямом и в обратном направлении по часам космонавта составит .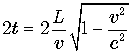

Время наблюдателя A будет идти медленнее и за время обратного пути космонавта изменится всего лишь на 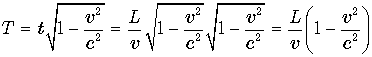. Но этот результат мы не можем использовать, так как не знаем начальных показаний часов наблюдателя A в начале обратного путешествия космонавта. В начале обратного путешествия космонавта мы знаем только показания часов в пункте B, а это не одно и то же. С точки зрения космонавта все часы на Земле вдоль оси x показывают разное время. Самый простой способ узнать показания часов земного наблюдателя в момент его встречи с космонавтом – это перейти на его точку зрения. С точки зрения земного наблюдателя по его часам к этому моменту пройдет времени . Следовательно, в момент встречи мы снова получаем .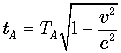

Движущиеся синхронизированные часы с точки зрения неподвижного наблюдателя

При анализе парадокса близнецов и решении многих других задач по релятивизму известную трудность вызывает тот факт, что показания часов движущейся системы, синхронизированных в этой системе, для неподвижного наблюдателя представляются различными. Остановимся на этом эффекте подробнее.

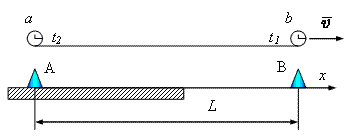
Вернемся снова к точке зрения земного наблюдателя. Пусть часы a и b принадлежат подвижной системе и они синхронизированы в этой системе. Когда часы b проходят над наблюдателем B часы a проходят над наблюдателем A. Пусть кроме того часы земного наблюдателя начали свой отсчет в тот момент, когда часы b проходили над наблюдателем A. Тогда в тот момент, когда часы b пройдут над пунктом B, часы земного и космического наблюдателя будут показывать соответственно

, .

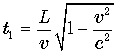В этот же момент над наблюдателем A проходят часы подвижной системы координат t₂. Иначе можно сказать, что часы t₂ прошли над наблюдателем A, когда его часы показывали время . Теперь перейдем в подвижную систему координат. С точки зрения подвижного наблюдателя все его часы показывают одно и то же время. Кроме того ему известно, что в момент встречи часов t₂ и наблюдателя A, часы наблюдателя A показывали время . Но часы наблюдателя A идут медленнее его собственных часов. Следовательно его часы (любые, а значит и t₂) должны показывать в момент встречи время 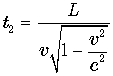. Именно этот результат и должен увидеть земной наблюдатель в пункте A.

Запишем оба выражения рядом:

,

.

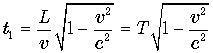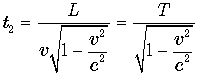Видно, что с точки зрения земного наблюдателя подвижные синхронизированные часы показывают разное время. Найдем разницу в их показаниях.

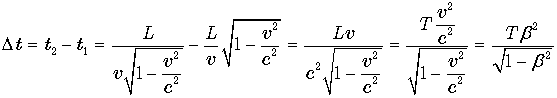, где .

Запомним этот результат.

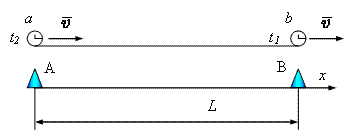
Если двое синхронизированных в своей системе отсчета часов t₁ и t₂ движутся относительно неподвижной системы со скоростью , а расстояние между ними равно L в неподвижной системе, то они показывают разное время. Причем

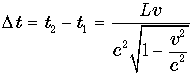, где  – разница в показаниях подвижных часов.

Та же самая разница по часам неподвижного наблюдателя будет равна

.

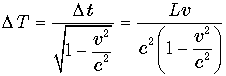При этом отстающие часы показывают опережающее время: t₂ > t₁.

Еще одно полезное замечание.

Из полученных выражений видно, что если наблюдатель на Земле будет следить за часами удаляющегося наблюдателя, то заметит, что они отстают от его часов: 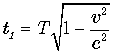. А если он будет следить за часами движущейся системы, которые проносятся непосредственно над ним, то эти часы будут опережать время на Земле: .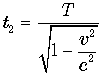

Теперь вернемся к задаче о близнецах и решим ее еще одним способом.

Еще один способ решения парадокса близнецов

Расставим в каждой точке подвижной системы координат часы и синхронизируем их. Пусть наблюдатель в точке A следит за проносящимися над ним часами.

Пусть в тот момент, когда часы t₁ находились на расстоянии L, часы t₂ над – наблюдателем A, и часы наблюдателя A показывали время , подвижная система остановилась. ... Оказывается, что мы не можем так сказать. Протяженную подвижную систему можно остановить не одним, а многими способами и с каждым из способов связаны некоторые проблемы. Мы в данной задаче будем считать, что система останавливается мгновенно по наблюдениям из сопутствующей системы в тот момент, когда вторые часы проходят над пунктом наблюдения A. Поскольку в сопутствующей системе все часы космонавта показывают одинаковое время, все они в момент остановки будут показывать то же самое время, что и часы t₂ в момент достижения пункта A.

В земной системе отсчета часы t₁ и  t₂ показывают разное время, причем часы t₁ отстают, следовательно, после остановки часов t₂ они будут продолжать движение.

В момент остановки часов  t₂ показания часов в земной системе координат были следующие:

,

.

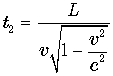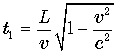Следовательно, часы t₁ после остановки часов t₂ будут двигаться еще

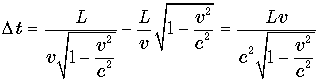 по их собственному времени,

как мы уже отмечали.

На Земле при этом пройдет

.

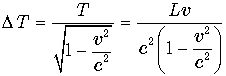За это время часы t₂ в земной системе координат пролетят расстояние

.

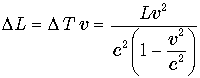Следовательно, в момент своей остановки часы t₁ будут находиться на расстоянии

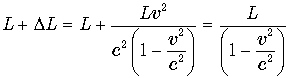 от пункта A

и будут показывать время

.

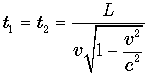Часы же на Земле покажут в этот момент время

.

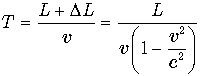Следовательно, и в этом случае часы космонавта показывают время меньшее, чем часы земного наблюдателя:

.

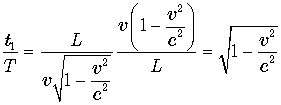На обратном пути все происходит аналогично.

Основная причина недоразумений, связанных с парадоксом часов или близнецов, вызвана кажущейся симметрией картины, которую могут наблюдать близнецы. В действительности настоящей симметрии здесь нет. Космонавт улетает, и пока он летит, картина действительно симметричная: либо он летит, а брат покоится, либо наоборот. Дальше возможны два варианта развития событий: либо космонавт цепляется за систему отсчета Земли и на ней остается, либо землянину надоедает сидеть дома и он перепрыгивает на проносящуюся мимо него систему отсчета космонавта. От того, какой вариант изберут наши герои, зависит, кто из них будет моложе.

Вернемся к предыдущей задаче. Пусть в тот момент, когда над наблюдателем A пролетали часы t₂, он за них зацепился и остался в системе космонавта. В этот момент его часы показывали , а часы 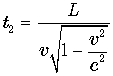. Следовательно, перейдя на космический корабль, землянин оказывается моложе своего брата-космонавта.

Симметричная версия парадокса близнецов

Традиционная версия парадокса близнецов, предложенная Полем Ланжевеном, изначально не симметрична. Один из близнецов остается на Земле и ничего не делает, а второй сначала улетает, затем поворачивает и возвращается обратно. Мы можем сказать, что активная жизненная позиция позволяет второму брату лучше сохраниться. Конечно, мы понимаем, что дело здесь в другом, но то, что из ассиметричного условия вытекает ассиметричный результат – вполне закономерно.

Рассмотрим идеально симметричную версию парадокса.

Пусть близнецов будет трое. Один из них, так же как и раньше, не любит летать. Он нам пригодится только как сторонний наблюдатель. В принципе без него можно обойтись. Два других брата разлетаются с Земли одновременно в разные стороны с одинаковой скоростью и останавливаются на одинаковом от нее расстоянии в точках A и B. Затем они поворачиваются и возвращаются с той же скоростью на Землю. Пролетая над Землей, они могут сверить часы, и земной брат результаты этого сравнения может засвидетельствовать. Что же это сравнение даст? По наблюдениям земного наблюдателя часы обоих космонавтов должны показывать одинаковое время. По наблюдениям космонавта A относительно него двигается космонавт B и его часы должны показывать меньшее время. С другой стороны, космонавт B вправе считать, что относительно него двигается все время космонавт A и его часы должны показывать меньшее время. Что же в действительности они увидят, когда сравнят часы?

Задачу можно разбить на два этапа. На первом этапе космонавты разлетаются. На втором летят обратно. Полное решение получается длинным. Сосредоточим наше внимание на наиболее драматичном заключительном этапе путешествия. Будем считать до пунктов A и B братья как-то добрались, и при этом часы всех трех братьев показывают одинаковое время. Этого можно добиться, если двигаться очень медленно. Выйдя на свои исходные позиции на расстоянии L от Земли, братья разворачивают свои корабли. Одновременно по команде с Земли они начинают свое возвращение.

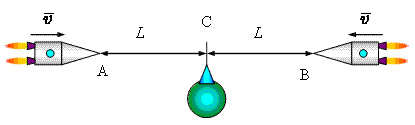
Точка зрения земного наблюдателя

Картина является полностью симметричной и оба космонавта встретятся на Земле через . В момент встречи часы космонавтов будут показывать одинаковое время .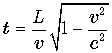

Поскольку все трое космонавтов смогут в этот момент непосредственно наблюдать часы друг друга, то этот результат они должны зарегистрировать все. На этом задачу можно было бы закончить. Правда, в этом случае остается неясно, как же это так получилось, что космонавты пришли к единому мнению.

Рассмотрим события с точки зрения космонавтов.

Точка зрения космонавта A

Космонавт A какое-то время, находясь в точке A, покоился относительно Земли, как, впрочем, и космонавт B. Начало движения всегда сопряжено с ускорением. Ускоренное движение – это трудное место в специально теории относительности. Свою первую работу по специальной теории относительности Эйнштейн опубликовал в 1905 году. В этой работе Эйнштейн, в частности, делает вывод, что если некоторые часы из произвольной точки A были перенесены по произвольной замкнутой кривой, и опять были возвращены в исходную точку, то они отстанут от других таких же часов, которые все это время покоились в точке A. Поль Ланжевен в 1912 году, как мы уже отмечали, получает из этого результата парадокс близнецов. Эйнштейн в 1918 году публикует статью, в которой он в популярной форме объясняет этот парадокс. В этой статье Эйнштейн утверждает, в частности, что для разрешения парадокса близнецов необходимо привлекать общую теорию относительности.

Я не думаю, что этот совет нам чем-то поможет: общая теория относительности принципиально более сложная теория. Если мы для объяснения сравнительно простой задачи обратимся к общей теории относительности, мы окончательно запутаемся. Как и прежде мы будем пользоваться только элементарными приемами, но мы должны сознавать, что возможно не все, что мы делаем, выглядит в достаточной степени корректно.

Введем вспомогательную систему отсчета, которая движется со скоростью  по направлению от A к B.

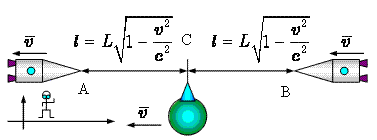
Если мы перейдем на эту систему, то увидим, что Земля вместе с находящимися в точках A и B кораблями движется на нас со скоростью . Расстояние же между Землей и кораблями при этом сократится до 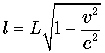. Но самое интересное, что мы увидим, это то, что часы в точках A, B и C показывают разное время. Часы B опережают часы C, а часы C опережают часы A на

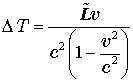 по часам вспомогательной системы.

При этом 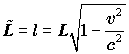, следовательно, .

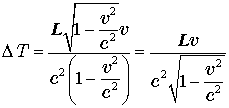Раз часы в точке B опережают, то корабль B начнет движение на 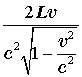 раньше, чем корабль A. Все это время корабль A будет продолжать оставаться в точке A и двигаться с одной скоростью вместе с Землей. Корабль B во вспомогательной системе будет двигаться со скоростью, которую можно вычислить по релятивистской формуле сложения скоростей .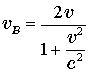

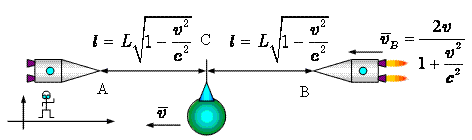
Так как точка C (точка встречи кораблей) во вспомогательной системе движется со скоростью , то корабль B к ней приближается со скоростью

.

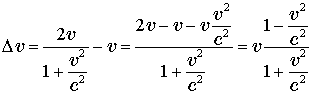Чтобы достичь точки C ему понадобится время

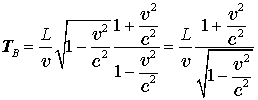, измеренное по часам вспомогательной системы.

По часам же космонавта B пройдет при этом

.

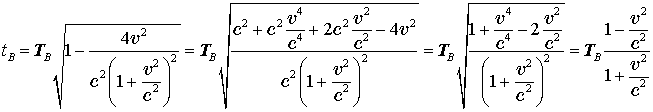Подставляя значение для , получим

.

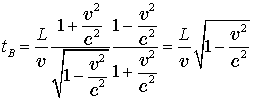Через 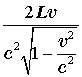 после начала движения корабля B начнет движение корабль A. С точки зрения вспомогательной системы это будет означать, что корабль A относительно нее остановится, и расстояние между кораблем и Землей начнет сокращаться со скоростью .

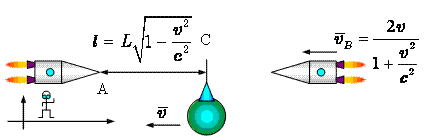
От начала старта корабля A и до встречи его с кораблем B в точке C по часам вспомогательной системы, а значит и по часам космонавта A пройдет времени

.

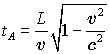Мы получили, что часы обоих космонавтов в точке их встречи показывают одинаковое время 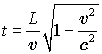. Таким образом, мы можем сказать, что точки зрения земного наблюдателя и наблюдателя A относительно показаний часов космонавтов совпали. Очевидно, что для космонавта B мы получим тот же самый результат.

Свой путь до точки C космонавт A преодолел за

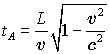, а космонавт B на это потратил 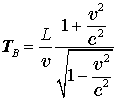, то есть на

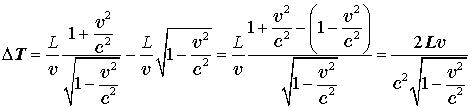 больше.

Но именно на это значение он стартовал раньше, следовательно, они действительно встретятся в точке C.

Какой вывод мы можем сделать из этого? Парадокса не получилось. Мнения всех наблюдателей совпали.

Аналогичным образом можно проанализировать и начальный этап развития событий, на котором космонавты добираются до пунктов A и B. Если решить задачу полностью, то мы снова получим, что тот близнец, который все время оставался на Земле окажется старше, а оба брата космонавта будут моложе и одного возраста.

Время в удаленных точках

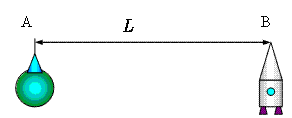
Пусть космонавт B находится в состоянии покоя относительно Земли на расстоянии L от нее в точке B. Часы космонавта и часы земного наблюдателя синхронизированы и показывают одинаковое время. Проследим, что скажет космонавт о часах наблюдателя A после старта.

Пусть космонавт стартует к Земле и мгновенно набирает скорость . Естественно, слово "мгновенно" означает только то, что период времени разгона или торможения должен быть существенно меньше тех эффектов с часами, о которых мы будем говорить. Отсюда с необходимостью следует, что расстояние L должно быть достаточно большим.

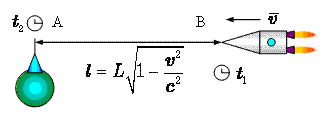
Приобретя скорость очень быстро, космонавт не должен заметить каких-то изменений в показаниях земных часов, находящихся в одном месте с ним, то есть в точке B. Следовательно, его часы и часы , оставшиеся на Земле, должны и после старта показывать одинаковое время.

Приобретя скорость  относительно Земли, космонавт вправе считать, что Земля движется к нему с этой скоростью. Отрезок AB, принадлежащий земной системе координат, стал короче 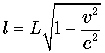, а часы и , синхронизированные в земной системе координат, показывают разное время. Если верить нашим предыдущим вычислениям, то

,

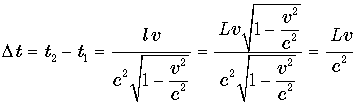следовательно, за время разгона космонавта часы  ушли вперед и показывают .

Нетрудно заметить, что если космонавт стартует в противоположном направлении, то часы земного наблюдателя отстанут на ту же величину.

Пока все    ?????  ?????    Пока все